Al aplicar la matemática
al estudio de la herencia, Mendel estaba declarando que las leyes de probabilidad
se aplican a la biología igual que a las ciencias físicas. Arrojemos una
moneda. La probabilidad de que salga cara es 50%, es decir, una posibilidad en
dos, o 1/2. La probabilidad de que salga cruz también es 50% o 1/2. La
probabilidad de que salga una o la otra es la certeza, o sea, una en una. Ahora
arrójense dos monedas, la probabilidad de que una caiga cara arriba es de
nuevo 1/2. La probabilidad de que la segunda caiga cara arriba es también 1/2.
La probabilidad de que ambas caigan cara arriba es 1/2 x 1/2 o 1/4. Así, la
probabilidad de que dos acontecimientos independientes ocurran simultáneamente
es simplemente la probabilidad de que uno ocurra solo multiplicada por la
probabilidad de que el otro ocurra solo. Esto se conoce como la regla del producto de las probabilidades. La
probabilidad de que ambas monedas caigan cruz arriba es, de modo semejante, 1/2
x 1/2 o 1/4. La probabilidad de que la primera moneda salga cruz y la segunda
salga cara es x y la probabilidad de que ambas salgan cruz es también
1/2 x 1/2.
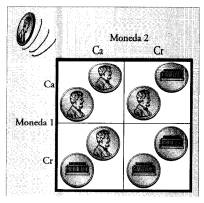
Podemos diagramar esto en un tablero o
cuadro de Punnett — como muestra la figura— en el cual la combinación de cada
casilla tiene igual probabilidad de ocurrir. De modo semejante, en el
experimento de Mendel diagramado en la figura 12-8, la probabilidad de que un
gameto producido por una planta F2 de genotipo Rb lleve el alelo B
es 1/2 y la probabilidad de que lleve el alelo b es 1/2. Por lo tanto, la probabilidad
de cualquier combinación específica de los dos alelos en la progenie —o sea,
BB, Bb, bB o bb— es 1/2 x 1/2 o 1/4. Fue indudablemente la observación de
que 1/4 de la progenie de la generación F2
mostraba el fenotipo recesivo lo que indicó a Mendel que estaba
observando un caso simple de las leyes de la probabilidad.
Volviendo al caso de
nuestras monedas, si intervinieran tres monedas, la probabilidad de que
aparezca cualquier combinación sería simplemente el producto de las tres posibilidades
individuales 1/2 x 1/2 x 1/2, o 1/8. De modo semejante, con cuatro monedas la
probabilidad de cualquier combinación específica es 1/2 x 1/2 x 1/2 x 1/2, o
1/16. El cuadro de Punnett de la figura expresa la probabilidad de cada una de
las cuatro combinaciones fenotípicas posibles.
Ahora bien, cuando hay
más de un ordenamiento posible de los acontecimientos que producen el
resultado especificado, se suman las probabilidades individuales. Por ejemplo,
¿cuál es la probabilidad de que se presenten cara y cruz en cualquier
secuencia? Hay dos maneras de que suceda esto: obteniendo primero cara (Ca) y
luego cruz (Cr) —lo que podemos expresar como (CaCr)— o cruz primero y luego
cara, es decir (CrCa). La probabilidad de obtener una cruz y luego cara, o una
cara y luego cruz, es la suma de sus probabilidades individuales (1/2 x 1/2) + (1/2 x 1/2) = 1/4 + 1/4 = 1/2. Esto se conoce como la regla de la suma de las probabilidades. En la cruza diagramada en la figura
12-8, se produce un heterocigoto del tipo Bb o del tipo bR. La probabilidad de
un heterocigoto en la generación F2 es, entonces, la suma de las
probabilidades de ambas combinaciones posibles: 1/4 + 1/4 = 1/2.
La regla de la suma de
las probabilidades, al igual qu la regla del producto, se aplica también a
casos mas complejos. Por ejemplo, si se pidiera la probabilidad de obtener dos
caras y una cruz, la respuesta sería 3/8. Hay tre combinaciones posibles:
CaCaCr, CaCrCa y CrCaCa. Par cada una de estas tres combinaciones, la
probabilidad e 1/2 x 1/2 x 1/2 = 1/8,
o sea, el producto de tres lanzamientos independientes. Así, la probabilidad de
obtener dos caras y una cruz es 1/8 + 1/8
+ 1/8 = 3/8.
Nótese que al planear sus experimentos, Mendel
hizo varias suposiciones: 1) para cada gen, la mitad de los game tos masculinos
producidos contenía uno de los aletos paternos y la otra mitad, el otro; 2)
para cada gen, la mitad de los gametos femeninos producidos contenía uno de lo
alelos maternos y la otra mitad, el otro, y 3) los gameto masculinos y
femeninos se combinan al azar. De esta manera pudieron aplicarse las leyes de
la probabilidad: un elegante matrimonio de la biología y la matemática.
|
|
Si uno arroja dos monedas cuatro veces, es
improbable que se obtengan los resultados precisos diagramados aquí. Sin embargo,
si uno arroja dos monedas cien veces, se aproximará a las proporciones que
predice el cuadro de Punnett y si uno tira dos monedas al aire mil veces, se
estará muy cerca de/ resultado teórico. Como Mendel sabía, la relación de
dominantes a recesivos en la generación E2 puede no ser
claramente visible si se trabaja con una muestra pequeña. Cuanto mayor sea
la muestra, sin embargo, más se ajustará a los resultados pronosticados por
las leyes de la probabilidasd |
Bibliografía
. Helen Curtis. “Biología” . Sexta edición.
Editorial Medica Panamericana. 2000. pag. 314